👩🏻🌾
Chap 4. The Greedy Approach 본문
Greedy Algorithm
-매 순간 가장 좋아보이는 것을 고르는 방법
General Greedy Approach
- 빈 집합으로 시작하여 집합 인스턴스에 대한 답을 나타낼 때까지 집합에 아이템을 순서대로 추가
- 선택 절차 ( = Selection Procedure)
- 그리디 기준에 따라 집합에 추가할 다음 아이템을 선택
- 타당성 확인 ( = Feasibility Check)
- 인스턴스에 답을 제공하는 방식으로 집합을 완료할 수 있는지 여부를 확인
- 답 확인 ( = Solution Check)
- 새 집합이 인스턴스에 대한 답을 구성하는지 여부를 결정
Minimum Spanning Trees
정의
- Undirected Graph
- Connected Graph
- Acyclic Graph
- Tree
- Spanning Tree for undirected graph
- G의 모든 정점을 포함하고 트리인 연결된 서브그래프
- Minimum Spanning Tree for undirected graph
- 최소 무게를 가진 G의 Spanning Tree

왼쪽에 사진을 보면 G1 그래프에서 나올 수 있는 4개의 subgraph (= G2, G3, G4, G5)가 있다.
G2 : V3-V4-V5가 cycle을 형성하므로 spanning tree X
G3, G4, G5 : spanning tree의 조건을 모두 만족 -> G3의 weight = 15, G4, G5의 weight = 10
따라서, G1의 Minimum Spanning Tree는 G4와 G5가 된다.
Prim's Algorithm
- MST구현에 사용되는 알고리즘으로 시작 정점에서 정점을 추가해가며 단계적으로 트리를 확장하는 기법
- 탐색 정점에 대해 연결된 인접 정점들 중 무게가 가장 작은 간선으로 연결된 정점을 선택

위 사진으로 Prim's Algorithm을 이해해보자.
- V1을 시작 정점으로 V1에 연결된 간선 중 무게가 1로 가장 작은 간선으로 연결된 V2를 선택한다.
- 이제 V1과 V2에 연결된 정점들 중 무게가 가장 작은 간선으로 연결된 정점인 V3을 선택한다. 이때, 간선을 선택할 수 있는 경우는 2가지이므로 둘 중 하나를 선택하면 된다.
- 탐색 정점에 연결된 인접 정점들 중 무게가 가장 작은 간선으로 연결된 정점을 선택하는 과정을 반복하여 모든 정점들이 선택되도록 한다.
Prim's Algorithm을 구현하기 위해서 다음과 같은 배열들을 사용한다.
- W[i][j] : 무게 정보 (symmetric)
- nearest[i] : Vi에 가장 가까운 Y에 존재하는 정점의 인덱스
- distance[i] : Vi와 nearest[i] 사이의 무게
public static set_of_edges prim(int n, const number W[][]){
index i, vnear;
index [] nearest = new index[2...n];
number min;
number[] distance = new number[2..n];
edge e;
set_of_edges F = ∅;
for(i = 2; i <= n; i++){
nearest[i] = 1;
distance[i] = W[1][i];
}
repeat(n-1) times { // 엣지를 n-1개 넣으면 돼서
min = ∞;
for(i =2; i <= n; i++){
if(0 <= distance[i] < min){
min = distance[i];
vnear = i;
}
e = edge connecting vertices indexed by vnear and nearest[vnear];
add e to F;
distance[vnear] = -1; // 고른 정점 표시
for(i = 2; i<= n; i++)
if(W[i][vnear] < distance[i]){
distance[i] = W[i][vnear];
nearest[i] = vnear;
}
return F;
}Time Complexity of Prim's Algorithm
Basic Operation : 두 개의 for문 내부에 존재하는 if문
Input Size : n ( = 정점의 개수)
T(n) = 2 * (n-1) * (n-1) ∈ 𝚯 (n^2)
Kruskal's Algorithm
- 마찬가지로 MST구현에 사용되는 알고리즘
- 그래프의 간선들을 가중치 기준으로 오름차순 정렬한 뒤, 정렬된 간선들 중 순서대로 사이클을 형성하지 않도록 간선들을 선택
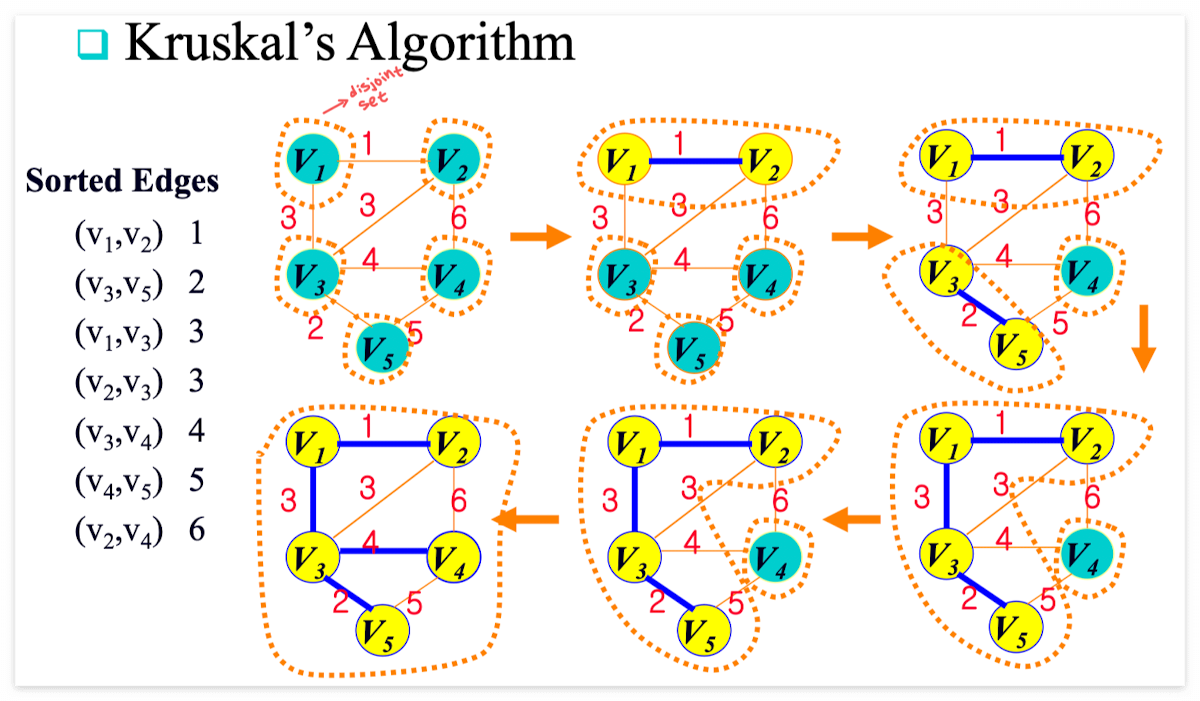
위 사진으로 Kruskal's Algorithm을 이해해보자.
- 간선들을 가중치 기준으로 오름차순으로 정렬한다
- (v1,v2)의 가중치가 가장 작으므로 해당 간선을 MST 집합에 넣는다.
- 그 다음으로 가중치가 적은 (v3, v5) 간선을 MST 집합에 넣는다.
- 다음은 (v1, v3)와 (v2, v3)의 가중치 값이 같으므로 (v1, v3) 간선을 MST 집합에 넣고, (v2, v3) 간선은 고려만 하고 버린다.
- MST 집합에 (n-1)개의 간선들이 존재할 때까지 간선 선택을 반복한다.
Kruskal's Algorithm을 구현하기 위해서 다음과 같은 함수들을 사용한다.
- Initial(n) : n개의 disjoing subset을 만들어주는 함수
- p = find(i) : 인덱스가 i인 정점이 어느 disjoint set에 포함되어 있는지 알려주는 함수
- merge(p, q) : 두 subset을 병합하는 함수
- equal(p, q) : 두 subset이 같은 집합에 속하는지 알려주는 함수, true 또는 false 반환
public static set_of_edges kruskal(int n, int m, set_of_edges E){
index i, j;
set_pointer p, q;
edge e;
set_of_edges F = ∅;
Sort the m edges in E by weight in nondecreasing order;
initial(n);
while(|F| < n-1){
e = edge with the least weight not yet considered;
i, j = indicesof vertices connected by e;
p = find(i);
q = find(j);
if(!Equal(p,q)){
merge(p, q);
add e to F;
}
}
return F;
}Time Complexity of Kruskal's Algorithm
Basic Operation : 비교 연산자
Input Size : n ( = 정점의 개수), m ( = 간선의 개수)
- Time to sort the edges
- W(m) ∈ 𝚯 (m lg m) using MergeSort
- Time in the while loop
- W(m) ∈ 𝚯(m lg m) using DisjoingSet implementation
- Time to initialize n disjoint sets
- T(n) ∈ 𝚯(n)
위 3개의 Time의 합
➡️ W(m, n) ∈ 𝚯(m lg m), n-1 ≤ m ≤ n(n-1) / 2
➡️ worst case : W(m, n) ∈ 𝚯(m lg m) = 𝚯(n^2 * lg n^2) = 𝚯(n^2 * lg n)
Huffman Code
- 데이터 압축을 위한 효율적인 인코딩 방법
- 가변 길이 이진 코드를 사용하여 텍스트 파일을 나타냄
텍스트 파일을 인코딩하기 위한 비트 수 = minimize ∑frequency(v) * depth(v)
for(i = 1; i < n; i++){
remove(PQ, p);
remove(PQ, q);
r = new nodetype();
r.left = p;
r.right = q;
r.frequency = p.frequency + q.frequency;
insert(PQ, r);
}
remove(PQ, r);
return r;
// nodetype info
Public class nodetype{
char symbol;
int frequency;
nodetype left;
nodetype right;
}remove() 함수 time complexity -> log n
insert() 함수 time complexity -> log n
Time complexity of Huffman Code
n * (3 * log n) 𝚯 n log n
'Study > Algorithm' 카테고리의 다른 글
| Chap 9. Introduction to the Theory of NP (0) | 2023.06.11 |
|---|---|
| Chap 7. Introduction to Computational Complexity: The Sorting Problem (0) | 2023.06.08 |
| Chap 6. Branch and Bound (0) | 2023.06.06 |
| Chap 5. Backtracking (0) | 2023.06.04 |
| Chap 3. Dynamic Programming (0) | 2023.04.20 |