👩🏻🌾
Chap 9. Introduction to the Theory of NP 본문
□Intractability
Polynomial-Time algorithm (다항시간 알고리즘)
- W(n) ∈ O(p(n))인 알고리즘이고, 이때 p(n)의 예시로는 2n, 3n^3 + 4n, n lg n 등이 있다.
ex) Insertion Sort, Sequential Search, etc
An Intractable Problem
- polynomial - time 알고리즘으로 해결이 불가능한 문제를 intractable이라고 불린다.
□The Three General Catagories of Problems
3 Categories of Problems
- Polynomial-Time algorithm found
- sorting, shortest paths problem, minimum spanning tree problem, etc
- Proven to be intractable
- non-polynomial 양의 결과를 필요로 하는 문제
- ex) 모든 Hamiltonian Circuits를 출력하는 문제, 모든 n값의 순열을 출력하는 문제
- Undecidable problem (컴퓨터로 풀 수 없는 문제)
- Halting Problem
- non-polynomial 양의 결과를 필요로 하는 문제
- Not proven to be intractable, but for which polynomial-time algorithms have never been found
- 0-1 Knapsack Problem, TSP problem, m-coloring problem, etc
□The sets P and NP
P
polynomial-time 알고리즘으로 해결 가능한 decision problem의 집합
-> TSP, 0-1 Knapsack는 P인지 모름
Verification(검증)
- 주장된 solution들이 실제로 decision problem이 맞는지 확인하는 과정
- 검증 단계에서 'false'를 반환하는 것은 decision problem인지에 대한 답으로 'no'인 것이 아니다.
- 다항 시간 검증 가능성이 기존의 decision problem이 다항 시간에 해결할 수 있음을 의미하지는 않는다.
Nondeterministic Algorithm
- 다음 단계를 가진 알고리즘
- Guessing(Nondeterministic)
- 문제의 인스턴스가 주어지면 이 단계는 단순히 답에 대한 추측인 문자열 S를 생성한다.
- Verification(Deterministic)
- 이 단계에 대한 입력으로 문자열 S가 주어지면
(a) 결국 "true"로 중단함 (b) "false"로 중단함 (c) 전혀 정지하지 않음(즉, 무한 루프)
- 이 단계에 대한 입력으로 문자열 S가 주어지면
Solve
- nondeterministic 알고리즘이 다음과 같은 경우에 decision problem를 "solve"한다고 말합니다.
1. 대답이 "yes"인 인스턴스의 경우, 검증 단계에서 "true"를 반환하는 문자열 S가 있다.
2. 대답이 "no"인 인스턴스의 경우, 검증 단계에서 "true"를 반환하는 문자열 S가 없다.
Polynomial-time nondeterministic Algorithm
- 검증 단계가 다항시간 알고리즘인 nondeterministic 알고리즘
NP
- polynomial-time nondeterministic 알고리즘으로 해결 가능한 decision problem의 집합
ex) The Traveling SalesPerson Decision Problem, The 0-1 Knapsack Decision Problem, The m-coloring Decision Problem, All problems in P
P⊂NP
□NP-Complete Problems
NP-Complete Problems
- NP의 문제 집합인 S의 구성원 중 하나가 P에 존재하면, 다른 모든 구성원도 P에 포함된다.
ex) The Traveling SalesPerson Decision Problem, The 0-1 Knapsack Decision Problem, The CNF Satisfiability Problem
The CNF Satisfiability Problem
- CNF에 있는 표현을 참으로 만드는 변수의 일부 진리 할당이 있는지 확인
이때, CNF는 Conjunctive Normal Form로 AND(∧) 연산자로 구분되는 일련의 clause(= 절)이다.
NP에 있는 문제라면 이것은 P에도 존재하는가?
아무도 모른다.
⭐️ Steven Cook's Theorm
- CNF-Satisfiability가 P에 존재한다면, P = NP이다.
➡️ 많은 문제들은 동등한 CNF 문제로 변환될 수 있다.
Polynomial-time Many-One Reducibility(A∝B)
- decision problem A에서 decision problem B로 가는 polynomial-time transformation algorithm(다항 시간 변환 알고리즘)이 있는 경우, A는 B로 polynomial-time many-one reducible이다.
NP-Completeness
문제 B가 다음과 같은 경우 "NP-complete"이라고 불린다
1. NP 안에 존재하고
2. NP 안에 존재하는 다른 모든 문제 A에 대하여 A∝B가 성립할 때
Theorem 9.1
decision problem B가 P에 존재하고, A∝B이라면 decision problem A는 P에 존재한다.
➡️ 문제 B가 NP에 존재하고, NP에 존재하는 모든 다른 문제인 A에 A∝B라면 문제 B는 NP-complete이다.
➡️ Theorem 9.1에 의해, NP-complete이 P에 존재하면 P = NP이다.
Theorem 9.2
CNF-Satisfiability는 NP-complete이다.
Theorem 9.3
문제 C가 다음과 같은 경우 "NP-complete"이라고 불린다
1. NP 안에 존재하고
2. 다른 어떤 NP-complete 문제 B에 대하여 B∝C가 성립할 때
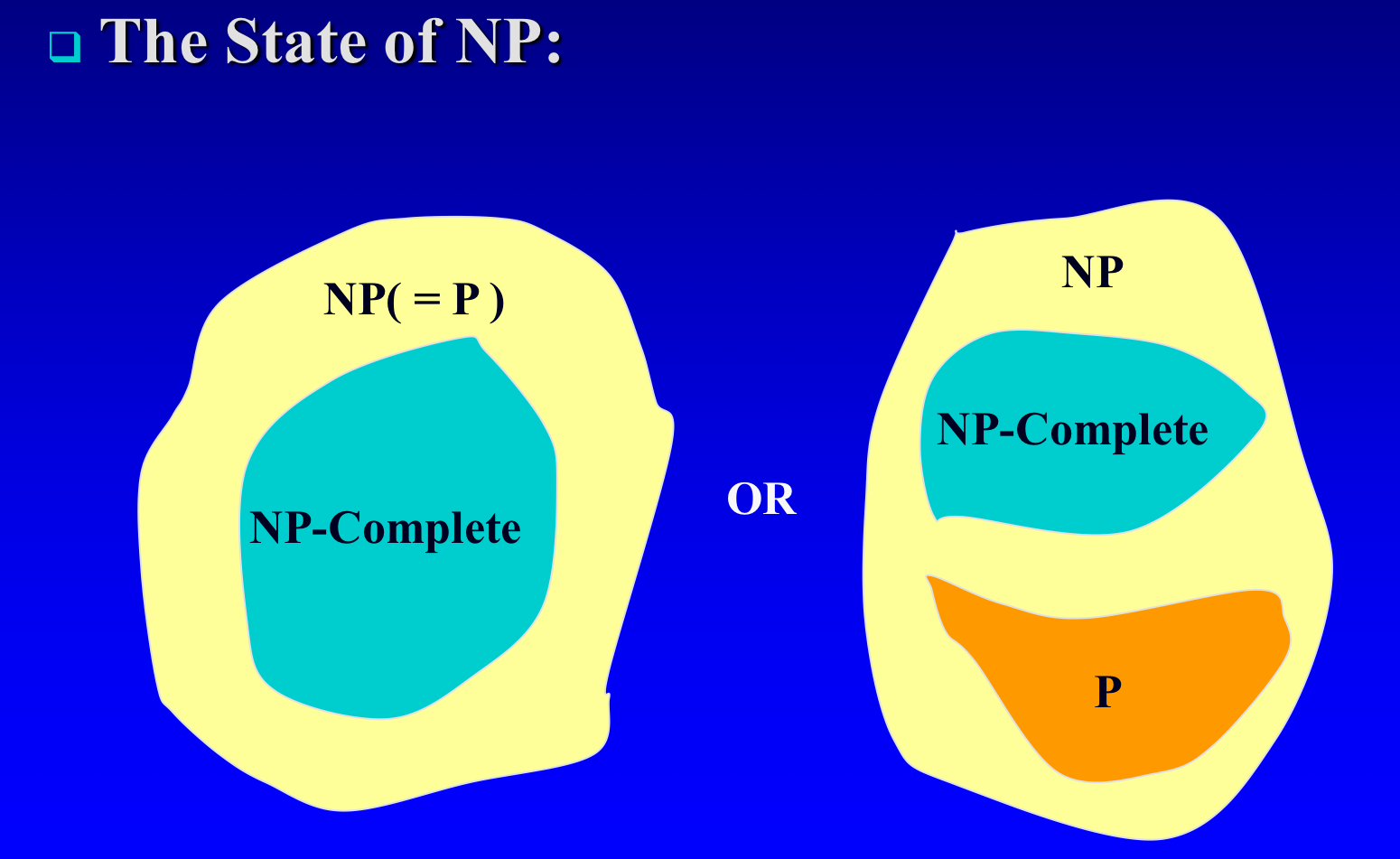
The State of NP
1. 만약 P = NP 라면, NPc ⊂ P 이다.
2. 만약 P ⊂ NP, NPc ∩ P = ∅ 이다.
□NP-Complete Problems
Polynomial-Time Turing Reducibility(A ∝T B)
문제 A가 B에 대한 가상 다항 시간 알고리즘을 사용하여 다항 시간 내에 풀 수 있는 경우 문제 A는 문제 B로 polynomial-time Turing reducible이다.
Notes
- 문제 B에 대한 다항 시간 알고리즘이 존재할 필요는 없다.
- 문제 A와 문제 B는 반드시 decision problems인 것은 아니다.
NP-Hard Problems
문제 B는 어떤 NP-Complete 문제 A가 A ∝T B라면 "NP-hard"라고 불린다.
'Study > Algorithm' 카테고리의 다른 글
| Chap 7. Introduction to Computational Complexity: The Sorting Problem (0) | 2023.06.08 |
|---|---|
| Chap 6. Branch and Bound (0) | 2023.06.06 |
| Chap 5. Backtracking (0) | 2023.06.04 |
| Chap 4. The Greedy Approach (0) | 2023.06.01 |
| Chap 3. Dynamic Programming (0) | 2023.04.20 |