👩🏻🌾
Chap 5. Backtracking 본문
728x90
Backtracking
해를 찾는 도중 막히면 이전 단계로 돌아가서 해를 찾아가는 기법
Backtracking을 사용하는 3가지 예시를 보자.
1. N-queens problem
- N x N 크기의 체스보드판에 N개의 퀸들을 서로 위협하지 않게 배치하는 문제
4 queens problem일 때
16개의 자리 중 4자리를 뽑는 경우 : C(16, 4) = 1820
두 퀸이 같은 행, 열 또는 대각선에 위치할 수 없으므로 배제할 수 있는 경우 : 4 x 4 x 4 x 4 = 256
<i,j> : i행 j열에 퀸이 위치
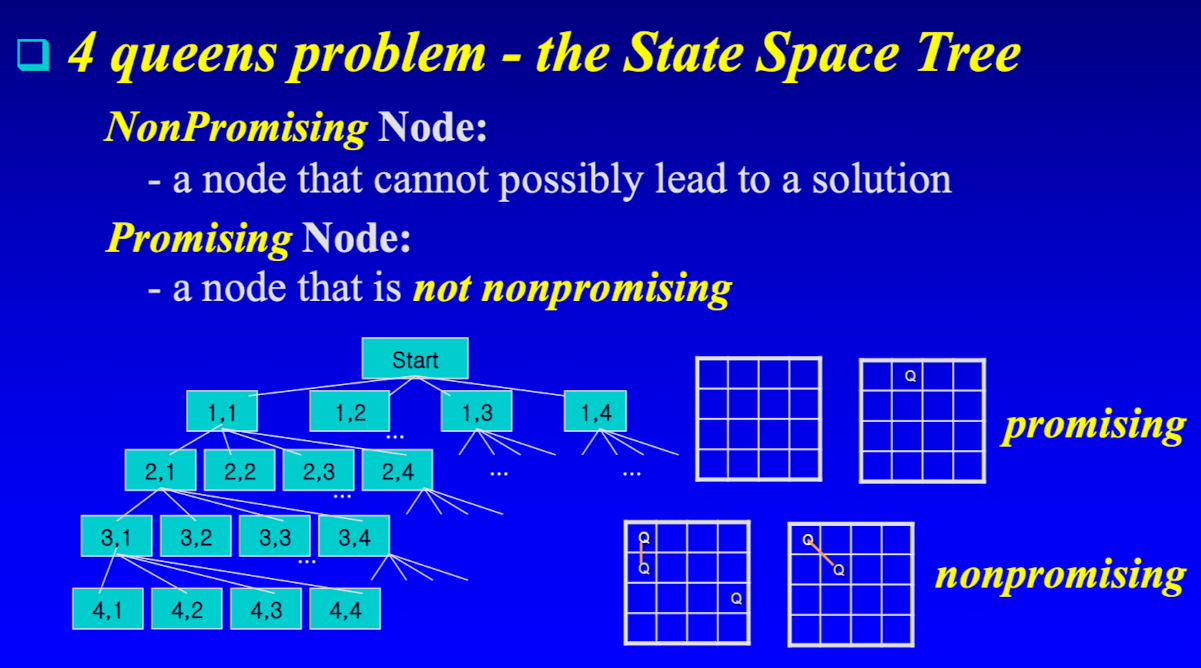
- 처음 시작할 때와, <1, 2>에만 퀸이 위치할 때 -> 하위 노드에서 답을 발견할 가능성이 있으므로 promising
- <1, 1> , <2, 1> , <3, 4>에 퀸들이 위치할 때, 같은 열에 위치하므로 답이 될 수 없으므로 nonpromising
- <1, 1> , <2, 2>에 퀸들이 위치할 때 또한 대각선에 위치하므로 nonpromising
각 노드들이 promising한지 확인하며 DFS 탐색한다. 만약 nonpromising이라면, 부모노드로 되돌아가서 다른 자식노드 탐색 시도한다.
➡️ Backtracking은 재귀적인 DFS 방식으로 구현될 수 있다.
public static void checknode(node v){
node u;
if(promising(v))
if(there is a solution at v)
write the solution
else
for(each child u of v)
checknode(u);
}
public static void queens(index i){
index j;
if(promising(i))
if(i == n)
system.out.print(col[1]...col[n])
else
for(j = 1; j <= n; j++){
col[i + 1] = j;
queens(i+1);
}
}
public static boolean promising(index i){
index k; boolean switch;
k = 1;
switch = true;
while(k < i && switch){
if(col[i] == col[k] || abs(col[i] - col[k] == i - k)
switch = false;
k++;
}
return swtich;
}2. The m-coloring problem
- 최대 m개의 서로 다른 색을 사용하여 방향이 없는 그래프를 인접한 두 정점이 같은 색이 되지 않게 색칠하는 모든 방법을 찾는 문제
3-coloring problem일 때

public static void m_coloring(index i){
int color;
if(promising(i))
if(i == n)
system.out.print(vcolor[1] .. vcolor[n]
else
for(color = 1; color <= m; color++){
vcolor[i + 1]= color;
m_coloring(i + 1);
}
}
public static bolean promising(index i){
index j; bool switch;
switch = true;
j = 1;
while(j < i && switch){
if(W[i][j] && vcolor[i] == vcolor[j]
switch = false;
j++;
}
}3. The 0-1 Knapsack Problem
knapsack의 상태
- current profit
- current weight
- the upper bound on the maximum profit -> item의 부분 조각을 허용하여 최대 이익을 구할 수 있다.

위 사진으로 knapsack problem의 state space tree를 이해해보자.
한 노드에 3가지의 값이 들어있는데 위에서부터 순서대로 '현재 이익, 현재 무게, 노드를 확장했을 때 가능한 최대이익'이다.
- 아이템을 아무것도 넣기 전에는 이익과 무게는 모두 0이고, 최대 이익은 item1의 값, item2의 값, item3의 값 * 9/10를 더해준 값이다. (이때, 최대 이익은 아이템의 부분조각을 허용했기 때문에 item3을 쪼개서 담을 수 있는 것이다.)
- 이제 item 1을 담았을 때와 담지 않았을 때의 노드를 보자.
- item1 in : item1의 가격과 무게를 더해주고 최대이익은 이전과 동일하다
- item 1 out : 부모노드와 달라지는 것은 최대이익이다. item1을 제외한 나머지 item들로 구할 수 있는 최대이익으로 값을 바꿔줘야한다. 이때, 바뀐 최대이익 값은 item2의 값, item3의 값, item4의 값 * 1/5의 합인 $82이다.
- 이런 식으로 3가지 값들을 업데이트 시킬 때, 총 무게가 16보다 크면 backtracking을 한다.
- node1까지 state space tree를 확장시키고 node2에서 item4를 담을 경우와 담지 않을 경우를 확장시켜야 하는데 node2의 최대이익이 $50이고, current best solution이 $90이다. node2를 더 확장해도 최대 이익이 $90에 미치지 못하므로 확장하지 않는다.
public static bool promising(index i){
index j, k; int totWeight; float bound;
if(weight >= W) return false;
else{
j = i + 1; bound = profit; totWeight = weight;
while(j <= n && totWeight + w[j] <= W){
totWeight = totWeight + w[j];
bound = bound + p[j];
j++;
}
k = j;
if(k <= n)
bound = bound + (W - totWeight) * p[k]/w[k];
return bound > maxProfit;
}
}728x90
'Study > Algorithm' 카테고리의 다른 글
| Chap 9. Introduction to the Theory of NP (0) | 2023.06.11 |
|---|---|
| Chap 7. Introduction to Computational Complexity: The Sorting Problem (0) | 2023.06.08 |
| Chap 6. Branch and Bound (0) | 2023.06.06 |
| Chap 4. The Greedy Approach (0) | 2023.06.01 |
| Chap 3. Dynamic Programming (0) | 2023.04.20 |
Comments